
The proper way of setting the pre-charge air pressure for a tank in operation is to isolate the tank from the system, drain off all expanded fluid, and measure the air pressure in the tank. The pre-charge air pressure can then be reset to its optimal setting. Depending on the tank size, this process can take a lengthy amount of time. To reduce the service time on an operating tank, there are alternative techniques that can be used.
Fixing a system expansion tank quickly requires some basic understanding of its operation and the principles of compressed gas (air). The expansion tank absorbs the system’s expanded fluid caused by temperature increase. The tank air volume controls the pressure increases in the system. A very large, oversized tank will register a very low pressure increase because the relative air cushion volume change is small. A properly sized expansion tank should show a pressure increase of 20-40 psi from empty to “full” of expanded fluid.
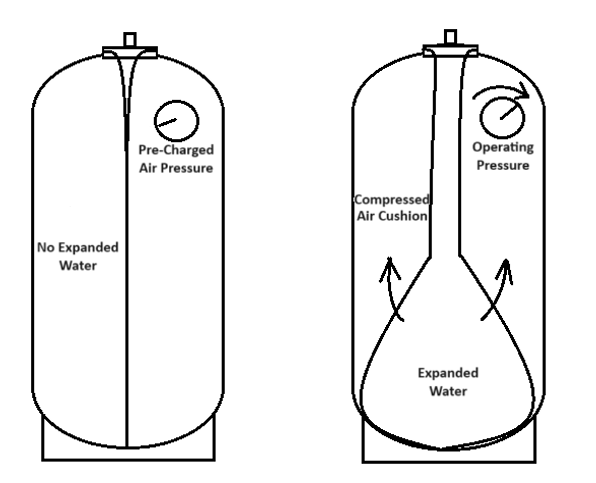
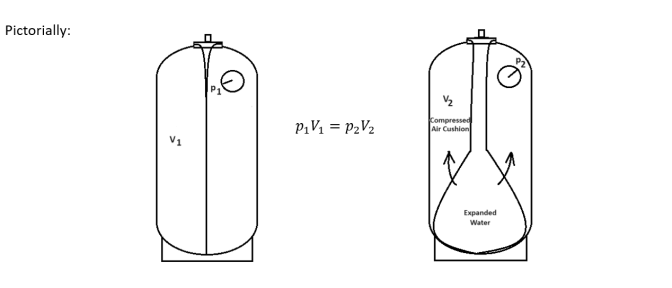
The air cushion in an expansion tank follows the principles of Boyle’s law. Boyle’s law states that pressure times volume of a contained gas equals a constant. If the compressed gas is pressurized to twice the starting pressure, the resulting volume of the compressed gas is 1/2 of the original volume. Simply stated, Boyle’s law is:
Air loss over time
Air or nitrogen gas can find its way out of the sealed tank. The points of minute air loss that may not be easily observed through standard bubble testing are threaded connections, the air charge valve, bulkhead fitting (bottom system connection on select tanks), and the bladder itself. The bladder is butyl, which has very low permeability. Higher pressure can drive more air through the bladder by means of diffusion. As the high-pressure water is “starved” for oxygen/air, it will pull molecules through the bladder over time.
As air is lost through the tank bladder or threaded connections, the result is the same as under-inflated air charge pressure. The tank will back fill with water until the air pressure in the tank equals the system water pressure. This will result in the same issues as an undersized expansion tank.
Annual Bladder Tank Check
Schedule a preventative maintenance event every 12 months. NOTE: there should be a drain valve between the system isolation valve and the tank. If one is not present, have one installed.
- Isolate the tank from the system.
- Drain the water from the bladder. Drain must be located between shut off valve and tank.
- Read the pre-charge air pressure. It should be approximately equal to ((static height above the tank)/2.31+10 psig), or the same as the pressure reducing valve setting (auto fill valve) feeding water to the system.
- Adjust to required pre-charge air pressure. If low, retest threaded connections with soap solution.
If pressure is within range, re-establish next PM event for 12-month period.
Setting the Pre-Charge “On-the-Fly”
With the tank in operation, a common question is “Can I adjust the pre-charge pressure in the tank without draining the tank first completely?” The answer to this question is “Yes,” providing we have working understanding of the compression air cushion of the expansion tank. As we approach the tank, we will notice that the tank is operating and the pressure P1. As we drain water from the isolated expansion tank and measure the captured water in a known volume bucket, a lower pressure P2 should be observed. Armed with these three data points, plus the size of the tank on the job, and the needed pre-charged pressure for the tank at startup, we can adjust the pressure P2 to ensure that, as the tank empties, it will ramp down to that required pre-charge pressure.
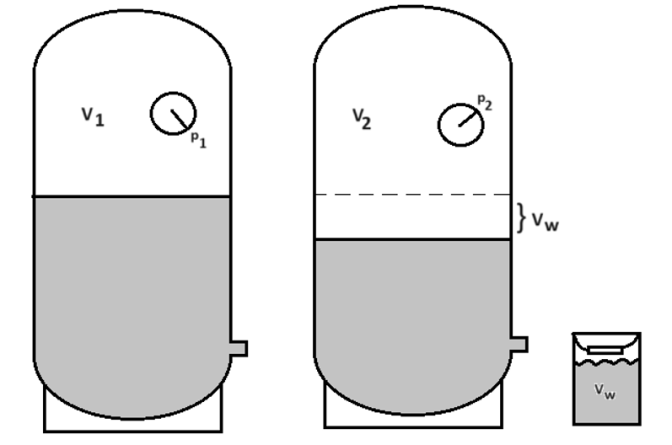
Let’s look at the variables needed to to be identified to set the pre-charge pressure with a somewhat full tank:
Vt Tank total volume in gallons.
Vw Water drawn from the operating expansion tank in gallons.
p1 Measured pressure before the water draw in psig.
p2 Measured pressure after the water draw in psig.
pa Atmospheric pressure (sea level typically 14.7 psia).
ppre Required tank pre-charge at system startup in psig.
With these known variables, we will calculate:
PE Potential energy needed in the tank in GAP (gallons absolute pressure in psia).
V1 Air volume of the operating expansion tank in gallons.
V2 Air volume of the expansion tank after the water draw in gallons.
The expansion tank can be thought of as a container of potential energy of (ppre + pa) x Vt at the startup of the system. Boyle’s law p1V1 = p2V2 means that this potential energy should remain the same at any condition of the tank. If we see that the potential energy has dropped, we can increase the air pressure in the tank until that potential energy is met.
We will first calculate the potential energy required by the tank’s air cushion, PE.
PE = (ppre + pa) x Tv
We will start with Boyle’s Law to help find V2 then adjust P2 to meet the required potential energy.
(p1 + pa)V1 = (p2 + pa)V2
As we draw off water, the resulting air cushion size relationship is:
V1 = V2-Vw (Vw is the known draw water volume)
Substituting shows:
(p1 + pa)(V2-Vw) = (p2 + pa)V2
Solving for V2:
V2 = Vw(p1 + pa)/(p1-p2)
Because we want the potential energy to match the tank’s empty condition, we solve:
(p2(new) + pa)V2 = PE
(p2(new) + pa) = PE/V2
p2(new) = PE/V2 – pa
Example: An NLA-800L (211 gallons) at the job site has a pressure reading of 60 psig. After isolating the tank and drawing off 8-gallons of water, the pressure reading drops to 52 psig. Atmospheric pressure is at sea level (pa = 14.7 psia). Find the required increase in pressure required after the draw of water to ensure the tank pre-charge pressure is 12 psig.
Vt Tank total volume 211 gallons
Vw Water drawn from the operating expansion tank 8 gallons.
p1 Measured pressure before the water draw 60 psig.
p2 Measured pressure after the water draw 52 psig.
pa Atmospheric pressure 14.7 psia.
ppre Required tank pre-charge at system startup 12 psig.
The potential energy at tank startup should be:
PE = (ppre+pa) x Vt
PE = (12+14.7) x 211 = 5,634 GAP (gallons absolute pressure in psia)
Solving for V2:
V2 = Vw(p1 + pa)/(p1-p2)
V2 = 8 (60 + 14.7)/(60-52)
V2 = 74.7 gallons
We can solve for the current potential energy in the air cushion V2 at pressure p2 of 52 psig and see that:
PE2 = (p2+pa) x V2
PE2 = (52+14.7) x 74.7 = 4,982 GAP (gallons absolute pressure in psia)
Now, determine the pressure p2(new) needed to bring the potential energy to the correct value of 5,634 GAP:
p2(new) = PE/V2 – pa
p2(new) = 5,634/74.7 – 14.7
p2(new) = 61 psig
It is important to reiterate that the best way to make sure the pre-charge pressure is correct is to drain the tank completely of any stored water and measure and adjust the pressure as needed. Often the method of drawing off a small amount of water will expedite the troubleshooting of an expansion tank at the job site. Regardless of findings and calculations, a tank should never be pressurized beyond the ASME working pressure of the tank. If calculations show that a high pressure is needed to reach the necessary potential energy, do not adjust if this could cause a dangerous or lethal situation. It is recommended that the entire tank be drained if this condition occurs.
Sam Fuller
Technical Engineer
Wessels Company
Download PDF Version of “How To: Quickly Adjust Vessel Pre-charge Pressure”
More →





 We are pleased to welcome Michele Curtis as the newest member of the Wessels team, joining our inventory department at the start of September. Michele brings a strong educational background from Ivy Tech, where she studied business and mathematics, along with several years of managerial experience in manufacturing at a snack company. Outside of work, she enjoys outdoor activities, weekend road trips, and fishing with her husband, as well as spending time with her granddaughter and watching football and baseball. An interesting note about Michele is that she is left-handed. Her colleagues, who share an office with her, appreciate her positive demeanor and ability to uplift the workplace atmosphere.
We are pleased to welcome Michele Curtis as the newest member of the Wessels team, joining our inventory department at the start of September. Michele brings a strong educational background from Ivy Tech, where she studied business and mathematics, along with several years of managerial experience in manufacturing at a snack company. Outside of work, she enjoys outdoor activities, weekend road trips, and fishing with her husband, as well as spending time with her granddaughter and watching football and baseball. An interesting note about Michele is that she is left-handed. Her colleagues, who share an office with her, appreciate her positive demeanor and ability to uplift the workplace atmosphere.


 The Wessels family is thrilled to welcome its newest team member, Sai Lian (pronounced “Sigh”), who joined our customer service team in December 2024. At just 18 years old, Sai brings a fresh perspective, infectious enthusiasm, and a passion for learning that makes him a perfect fit for our team. Sai’s interests include F1 racing, photography, and day trading. When he’s not assisting customers, you’ll find him cheering for Hawai’i volleyball and the Charlotte Hornets. With his fresh perspective and contagious energy, Sai is quickly becoming an invaluable part of the Wessels family, and we can’t wait to see all he’ll accomplish.
The Wessels family is thrilled to welcome its newest team member, Sai Lian (pronounced “Sigh”), who joined our customer service team in December 2024. At just 18 years old, Sai brings a fresh perspective, infectious enthusiasm, and a passion for learning that makes him a perfect fit for our team. Sai’s interests include F1 racing, photography, and day trading. When he’s not assisting customers, you’ll find him cheering for Hawai’i volleyball and the Charlotte Hornets. With his fresh perspective and contagious energy, Sai is quickly becoming an invaluable part of the Wessels family, and we can’t wait to see all he’ll accomplish.






 Wessels is proud to introduce our newest employee, Nathan Blank. He recently joined our Engineering Department as a Design Engineer. He graduated with a degree in mechanical engineering from Purdue University in Indianapolis. In his free time, he can be found playing Uncharted 4 and is rated as one of the top players in the world! He also enjoys watching Surf’s Up, weightlifting, and the Indy Fuel hockey team. Please join us in welcoming Nathan Blank to Wessels Company.
Wessels is proud to introduce our newest employee, Nathan Blank. He recently joined our Engineering Department as a Design Engineer. He graduated with a degree in mechanical engineering from Purdue University in Indianapolis. In his free time, he can be found playing Uncharted 4 and is rated as one of the top players in the world! He also enjoys watching Surf’s Up, weightlifting, and the Indy Fuel hockey team. Please join us in welcoming Nathan Blank to Wessels Company.





 At times, an expansion tank pre-charge must be increased using compressed air. Wessels recommends dry, oil-free air like the compressed air used in our factory, which is taken to below -50°F and processed through a dryer. Another option is to use compressed nitrogen because it is an inert gas that avoids oxidation and moisture content that can corrode the system. Nitrogen also provides more consistent pressure and is readily available. But how many cylinders are needed to pre-charge a bladder tank to the desired pressure? There are several factors that need to be considered: the size of the compressed gas cylinders, the size of the expansion tank accepting the nitrogen, and the pressure that is needed for the pre-charge.
At times, an expansion tank pre-charge must be increased using compressed air. Wessels recommends dry, oil-free air like the compressed air used in our factory, which is taken to below -50°F and processed through a dryer. Another option is to use compressed nitrogen because it is an inert gas that avoids oxidation and moisture content that can corrode the system. Nitrogen also provides more consistent pressure and is readily available. But how many cylinders are needed to pre-charge a bladder tank to the desired pressure? There are several factors that need to be considered: the size of the compressed gas cylinders, the size of the expansion tank accepting the nitrogen, and the pressure that is needed for the pre-charge.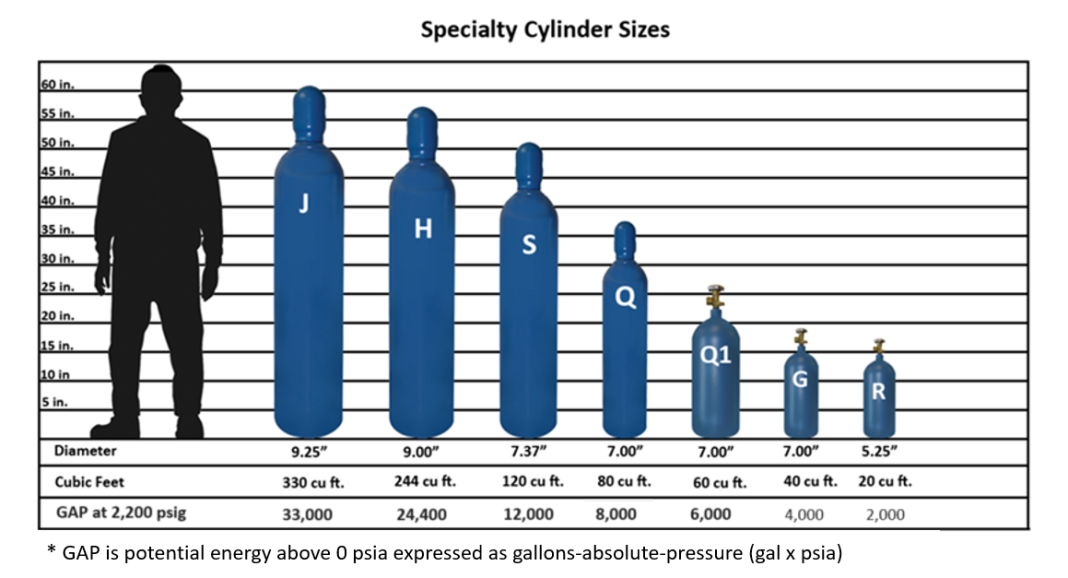
 Written by:
Written by: